整體壁板因其輕質(zhì)、高強(qiáng)、結(jié)構(gòu)效率等優(yōu)異的性能,被廣泛應(yīng)用于飛機(jī)機(jī)身、機(jī)翼部位等關(guān)鍵部件。目前,整體壁板常用的成形方法主要有噴丸、滾彎、壓彎、蠕變時(shí)效成形等[1-3]。在同等強(qiáng)度設(shè)計(jì)要求下,高溫鈦合金網(wǎng)格筋壁板相較于傳統(tǒng)的鋁合金筋壁板壁厚更小、筋的高寬比更大,并通常具有單/雙曲率的復(fù)雜曲面結(jié)構(gòu),屬于薄壁整體復(fù)雜結(jié)構(gòu)[4]。但由于高溫鈦合金多屬非時(shí)效強(qiáng)化型合金、加工溫度較高、加工窗口較窄、變形后回彈量大,采用常規(guī)冷變形或溫?zé)嶙冃畏椒ǔ尚纹渚W(wǎng)格筋整體壁板件對(duì)設(shè)備噸位要求較高、成形過(guò)程中易出現(xiàn)筋根部開(kāi)裂和筋條上端失穩(wěn)變形等成形缺陷,因此需探索新的成形方法。電脈沖輔助成形利用電致塑性效應(yīng)顯著降低成形載荷、提高材料的彎曲成形極限[5],有效避免成形過(guò)程中筋根部開(kāi)裂問(wèn)題;另一方面,可利用材料自阻產(chǎn)生的焦耳熱溫升快速提供熱變形條件,彌補(bǔ)變形過(guò)程中的熱損失,相較于電阻爐加熱有望顯著提高加熱速度、降低能源消耗與工裝成本[6]。然而,在電脈沖輔助成形過(guò)程中,由于電-熱-力場(chǎng)不均勻分布特征和網(wǎng)格筋整體壁板壓彎成形局部加載的特征,如電參數(shù)、變形參數(shù)、模具幾何參數(shù)和加載路徑設(shè)置不合理,可能導(dǎo)致壁板局部化變形嚴(yán)重、失穩(wěn)起皺、開(kāi)裂等缺陷。因此需要深入研究整體壁板電輔助成形變形行為,預(yù)測(cè)缺陷發(fā)生的時(shí)刻和位置,為整體壁板電輔助成形工藝設(shè)計(jì)提供依據(jù)。
關(guān)于整體壁板筋條失穩(wěn)預(yù)測(cè),國(guó)內(nèi)外眾多學(xué)者開(kāi)展了深入研究。Yan[7,8]等提出了一種基于能量法、彈塑性力學(xué)和數(shù)值分析的壓彎成形過(guò)程中加勁肋臨界屈曲載荷的求解方法,并對(duì)鋁合金高加勁肋整體板壓彎成形斷裂進(jìn)行預(yù)測(cè)。Mallela等[9]利用神經(jīng)網(wǎng)絡(luò)準(zhǔn)確預(yù)測(cè)了復(fù)合材料整體壁板的剪切失穩(wěn)載荷。Li[10]等提出了一種新的分析方法來(lái)預(yù)測(cè)加筋板在循環(huán)平面載荷作用下的非線性應(yīng)力應(yīng)變曲線,對(duì)船舶等大型箱梁結(jié)構(gòu)的漸進(jìn)倒塌分析提供基礎(chǔ)。Su[11]等研究了Ti6Al4V鈦合金加筋板在平面剪切載荷作用下的結(jié)構(gòu)行為。通過(guò)剪切試驗(yàn),得到了試件的屈曲失穩(wěn)、后屈曲過(guò)程和破壞機(jī)理,并研究了肋板厚度和肋板高度對(duì)加筋板性能的影響。Zhou[12]等建立了加筋板彈性屈曲分析的解析解,研究了加筋板主要幾何參數(shù)對(duì)其屈曲強(qiáng)度的影響。劉勁松[13]和任麗梅[14]等人對(duì)壓彎成形進(jìn)行了實(shí)驗(yàn)和數(shù)值模擬研究,分析了加勁肋的屈曲現(xiàn)象。然而,到目前為止,關(guān)于電脈沖輔助壓彎成形整體壁板屈曲研究還很少。
本研究首先建立了Ti55鈦合金整體壁板電脈沖輔助壓彎成形的有限元模型,分析成形過(guò)程中壁板不均勻溫度場(chǎng)分布及不同位置應(yīng)力應(yīng)變分布。并分析不同工藝參數(shù)和壁板幾何參數(shù)對(duì)筋條失穩(wěn)敏感性和筋條最終失穩(wěn)程度的影響,為鈦合金整體壁板電脈沖輔助壓彎成形設(shè)計(jì)提供依據(jù)。
1、有限元模型
1.1幾何模型和材料參數(shù)
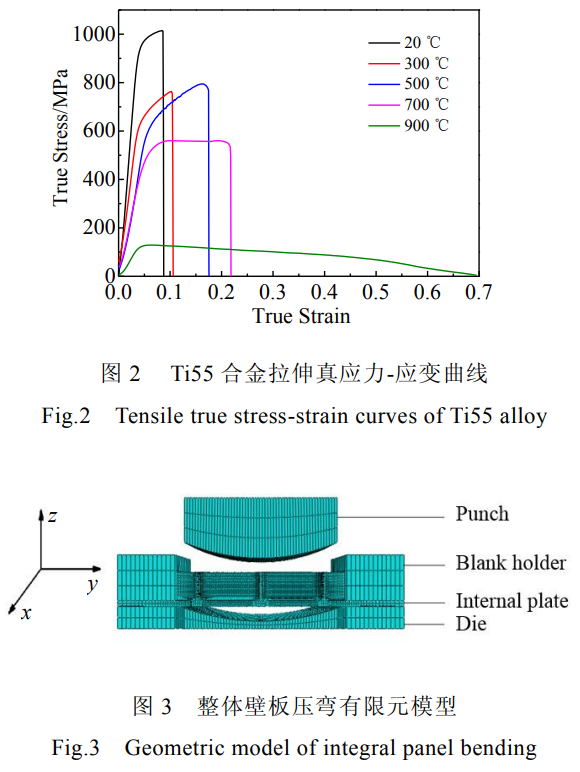
針對(duì)飛機(jī)整體壁板的典型結(jié)構(gòu),設(shè)計(jì)了一種多網(wǎng)格筋的整體壁板,整體壁板截面尺寸為100mm×50mm,厚度為12mm,其中蒙皮的厚度為2mm,加強(qiáng)筋寬度為1mm,加強(qiáng)筋之間橫向?qū)挾葹?1mm,縱向?qū)挾葹?6mm,如圖1所示。凹模長(zhǎng)寬高相應(yīng)為100mm×50mm×25mm,壓彎半徑分別為80、140、200mm,圓角過(guò)渡半徑為10mm,壓邊區(qū)域長(zhǎng)度為20mm。整體壁板材料為Ti55合金,其基本性能參數(shù)如表1所示。在拉伸機(jī)上進(jìn)行了應(yīng)變速率為0.01s-1單向拉伸實(shí)驗(yàn),得到了不同溫度下的應(yīng)力-應(yīng)變曲線如圖2所示。模型中塑性參數(shù)的定義取曲線中的應(yīng)力-應(yīng)變數(shù)據(jù)。
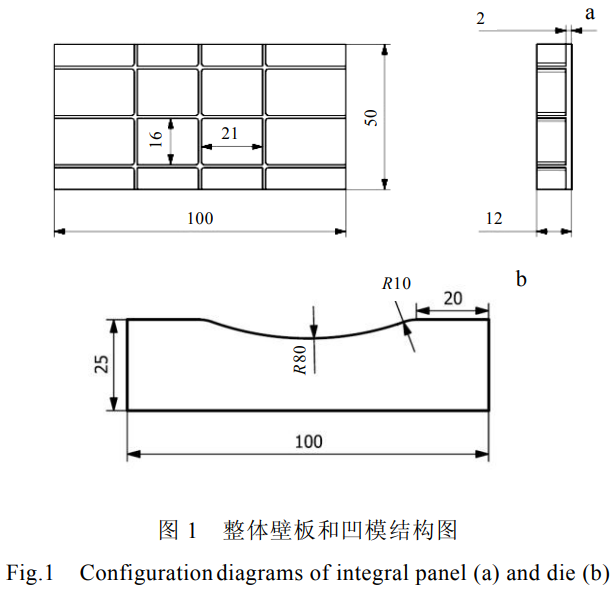
表1Ti55合金的熱物理性能參數(shù) Table1ThermophysicalperformanceparametersofTi55alloy
| Temperature/℃ | Thermalconductivity/W·m?1·K?1 | Specificheatcapacity/J·kg?1·K?1 | Coefficientoflinearexpansion/10??K?1 |
| 20 | 5.44 | 611 | 9.10 |
| 100 | 6.68 | 685 | 7.90 |
| 200 | 8.81 | 695 | 9.05 |
| 300 | 10.50 | 710 | 9.42 |
| 400 | 12.60 | 745 | 9.30 |
| 500 | 14.30 | 760 | 9.42 |
| 600 | 15.55 | 890 | 9.51 |
1.2模擬設(shè)置
通過(guò)有限元商業(yè)軟件ABAQUS熱電結(jié)構(gòu)耦合分析對(duì)Ti55網(wǎng)格筋整體壁板電脈沖輔助壓彎過(guò)程進(jìn)行數(shù)值模擬分析,建立的有限元模型如圖3所示。凸模和凹模均定義為實(shí)體,筋板與模具、外界環(huán)境之間的換熱系數(shù)設(shè)置為15W.m-2.K-1,設(shè)置凸凹模的表面為主面,板材的表面為從面。采用庫(kù)侖摩擦條件,設(shè)置沖頭、凹模以及壓邊塊與筋板之間的摩擦系數(shù)為0.3。模擬過(guò)程中,凹模和壓邊塊保持靜止不動(dòng),各方向的位移均設(shè)定為零,在壁板橫向兩端施加電流,并對(duì)沖頭施加指定速度加載條件,整個(gè)成形過(guò)程為40s,前20s為電脈沖加熱階段,后20s為壓彎過(guò)程,后續(xù)壓彎階段電流繼續(xù)對(duì)其加熱。網(wǎng)格劃分采用Q3D8R六面體單元,共有64274單元。
對(duì)5組不同工藝參數(shù)和幾何參數(shù)加筋板壓彎過(guò)程進(jìn)行了有限元模擬,分析了工藝參數(shù)(施加電流大小和加筋板壓彎半徑)和幾何參數(shù)(筋條寬高比、腹板厚度和橫筋間距)對(duì)加筋板失穩(wěn)屈曲的影響。各參數(shù)的取值范圍分別為:電流密度(7~9A/mm2);壁板壓彎半徑(60~100mm);筋條高度(9~10mm);腹板厚度(1~3mm);橫向筋條間距(11~41mm)。
2、結(jié)果與分析
2.1整體壁板溫度場(chǎng)分析
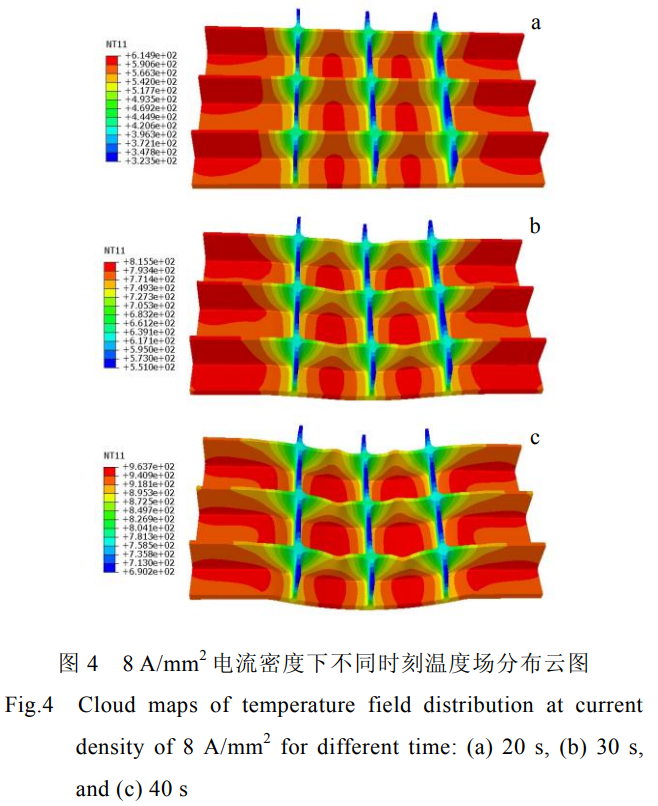
對(duì)施加電流密度7、8、9A/mm2的加筋板進(jìn)行有限元模擬,圖4為電流密度為8A/mm2時(shí)不同成形時(shí)間下的溫度場(chǎng)分布云圖。筋板橫向中心區(qū)域的溫度略高于兩側(cè)區(qū)域的溫度,因?yàn)檎w壁板的兩側(cè)始終和凹模、壓邊圈接觸,壁板會(huì)向模具傳熱,從而導(dǎo)致中心區(qū)域的溫度高于壁板兩側(cè)的溫度。剛開(kāi)始成形時(shí),橫向(y方向)筋條溫度與腹板的溫度相差不大,隨著沖頭的下壓,橫向筋條與沖頭接觸傳熱,導(dǎo)致最終成形時(shí)橫向筋條溫度比蒙皮溫度低。由于電流施加方式是在壁板橫向的兩側(cè)表面施加電流,縱向(x方向)筋條流經(jīng)電流比橫向筋條流經(jīng)電流少,產(chǎn)生的焦耳熱要少,縱向筋條處的溫度遠(yuǎn)低于其他位置的溫度。
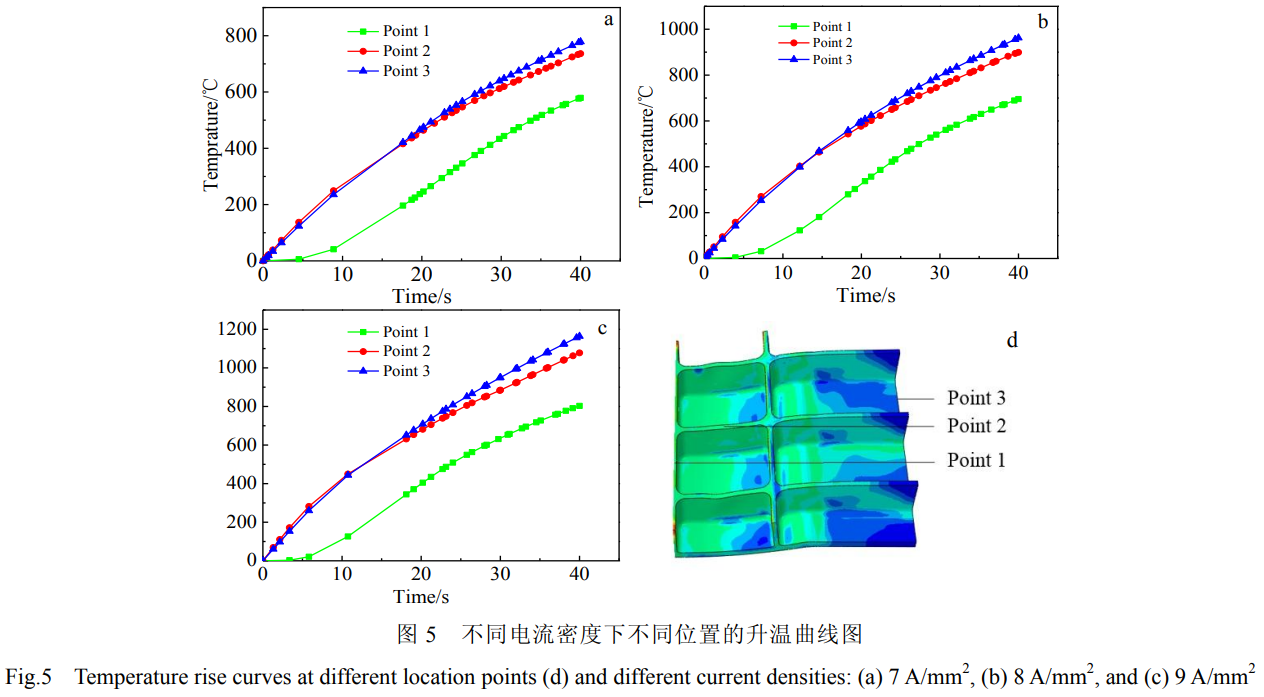
在整體壁板筋條橫筋處、筋條豎筋處、腹板中心處取3個(gè)溫度分析點(diǎn),如圖5所示。從升溫曲線圖可以看出電流密度為7、8、9A/mm2時(shí)筋板壓彎階段的溫度區(qū)間分別為494~786℃、615~963℃、727~1166℃。溫度過(guò)低時(shí)Ti55合金成形較為困難,溫度過(guò)高會(huì)導(dǎo)致氧化層的厚度較厚,當(dāng)電流密度為8A/mm2時(shí)筋板壓彎階段所處溫度區(qū)間最適宜。壁板蒙皮中心處(位置3)和橫向筋條處(位置2)在前20s時(shí)溫度一樣,但在后20s時(shí),沖頭下壓與壁板接觸產(chǎn)生熱傳導(dǎo),導(dǎo)致橫向筋條升溫速率下降,并且成形終了時(shí)橫向筋條溫度略低于腹板蒙皮處。由于整體壁板幾何結(jié)構(gòu)和電流加載方式,縱向筋條處區(qū)域溫度要比其它處區(qū)域低很多。
2.2壁板壓彎過(guò)程應(yīng)力應(yīng)變分析
圖6所示為在8A/mm2電流密度不同時(shí)間下的應(yīng)力應(yīng)變分布云圖。在成形的開(kāi)始階段(20s)時(shí),壁板一直處于電流加熱的狀態(tài),溫度上升導(dǎo)致壁板熱膨脹在中間位置產(chǎn)生一定的內(nèi)應(yīng)力。隨著模具的下壓,應(yīng)力開(kāi)始先增大,后面溫度進(jìn)一步的上升導(dǎo)致材料軟化,應(yīng)力反而呈下降的趨勢(shì)。最終應(yīng)力主要分布在壓彎的中心線和兩側(cè)壓邊塊的旁彎曲線上,并且由于縱向筋條溫度較低,縱向筋條處等效應(yīng)力值最大。在沖頭剛與筋板接觸時(shí),筋板未開(kāi)始變形,應(yīng)變?yōu)榱悖S著變形的增加,等效應(yīng)變不斷增大,等效應(yīng)變分布主要分布在橫向筋條和凹模圓角區(qū)域,而縱向條處和腹板處幾乎沒(méi)有等效應(yīng)變,表明其沒(méi)有產(chǎn)生塑性變形。
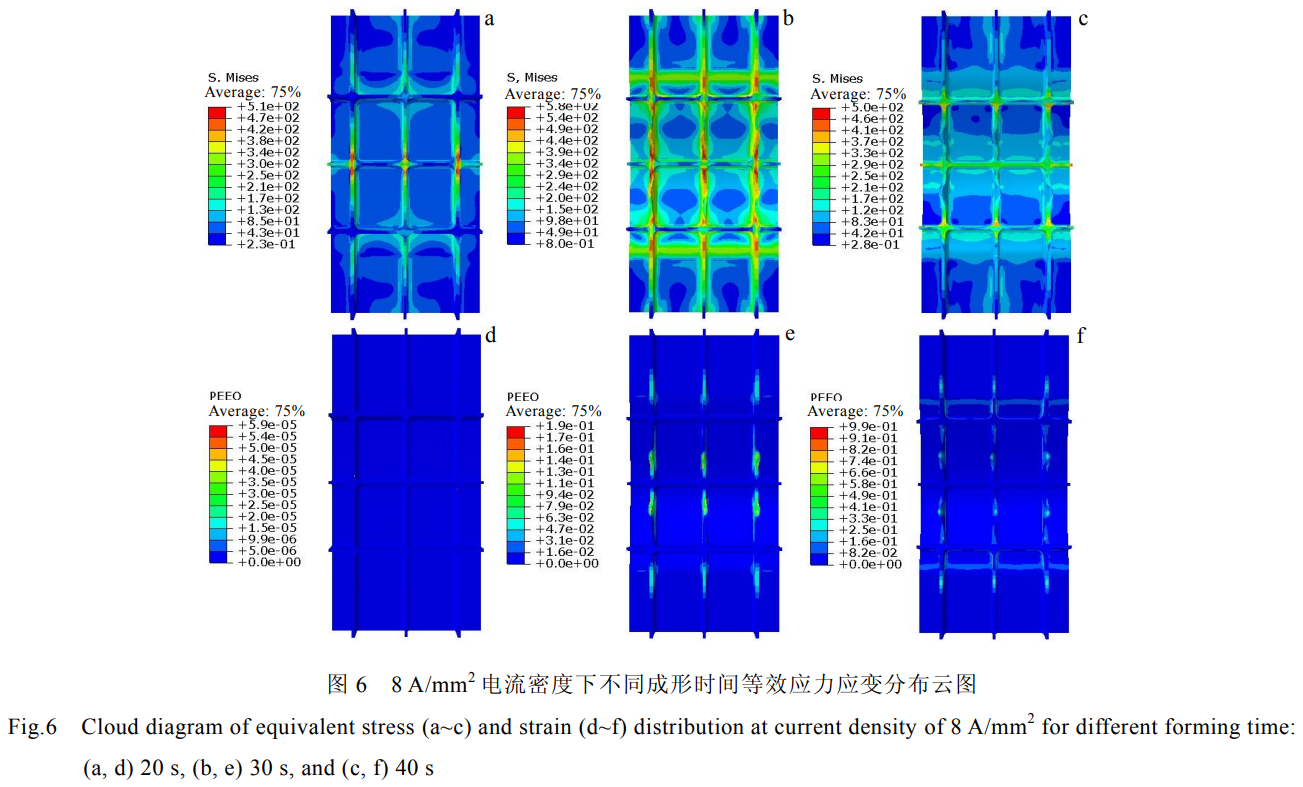
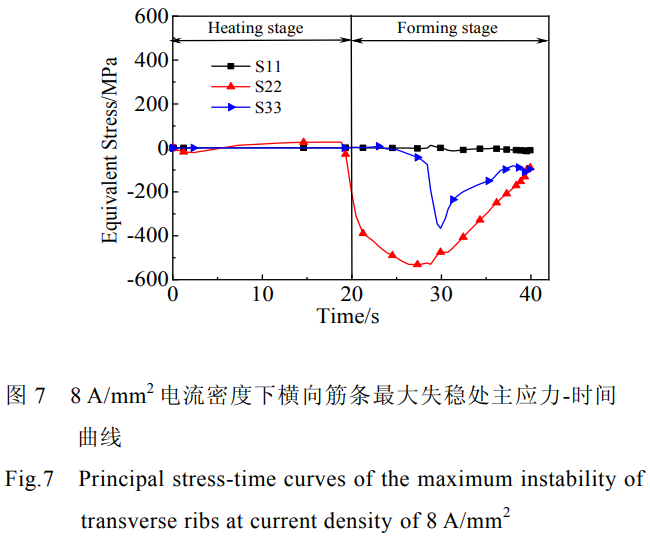
圖7所示為8A/mm2電流密度下橫向筋條最大失穩(wěn)處主應(yīng)力-時(shí)間曲線。由圖7可以看出整體壁板橫向筋條失穩(wěn)處x方向主應(yīng)力壓彎過(guò)程中一直為零,隨著沖頭的下壓壁板開(kāi)始彎曲變形,橫向筋條y方向壓應(yīng)力開(kāi)始迅速增加,這也是橫向筋條產(chǎn)生失穩(wěn)的主要原因。隨著壁板彎曲程度的加大,橫向筋條z方向壓應(yīng)力也隨著增加,后面由于橫向筋條溫度的上升,變形容易進(jìn)行,應(yīng)力值都呈下降的趨勢(shì)。
2.3電流密度對(duì)壁板失穩(wěn)屈曲的影響
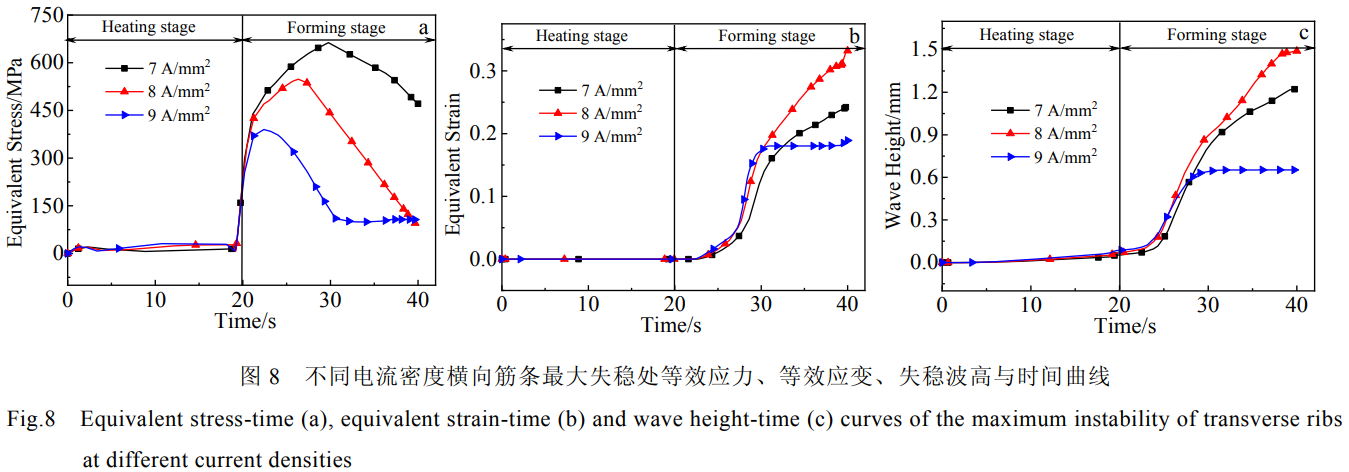
圖8所示為不同電流密度下橫向筋條失穩(wěn)處等效應(yīng)力、等效應(yīng)變、失穩(wěn)波高隨時(shí)間的變化曲線。由圖8a等效應(yīng)力-時(shí)間關(guān)系圖可知,在成形前20s時(shí),由于筋板只處于加熱階段,筋板未開(kāi)始變形,筋條處幾乎無(wú)應(yīng)力產(chǎn)生。電流加熱導(dǎo)致溫度的上升,整體壁板產(chǎn)生熱膨脹,沖頭實(shí)際和整體壁板接觸的時(shí)間在19s。隨著沖頭的下壓,應(yīng)力變化整體趨勢(shì)都是隨著變形的增加,應(yīng)力迅速上升,但是由于隨著溫度進(jìn)一步的上升,材料軟化導(dǎo)致應(yīng)力下降。電流密度越大,升溫速度越快,橫向筋條失穩(wěn)處的峰值應(yīng)力隨電流密度增加而減小。從圖8b可以看出應(yīng)變隨電流密度增加先增大后減小。電流密度大,整體壁板溫度高,筋條容易變形。但溫度繼續(xù)升高時(shí),整體壁板直接被壓彎,在橫向筋條上的應(yīng)力不足以讓其變形。電流密度為9A/mm2時(shí),成形的后10s中,應(yīng)力應(yīng)變幾乎無(wú)變化,也就是在壁板壓彎的最后10s過(guò)程中筋條沒(méi)有發(fā)生塑性變形。從圖8c可以看出,當(dāng)整體壁板其余參數(shù)一致時(shí),電流密度對(duì)筋條失穩(wěn)開(kāi)始的時(shí)刻沒(méi)有影響,只有當(dāng)壁板累計(jì)一定應(yīng)變量時(shí),筋條才開(kāi)始發(fā)生失穩(wěn)。
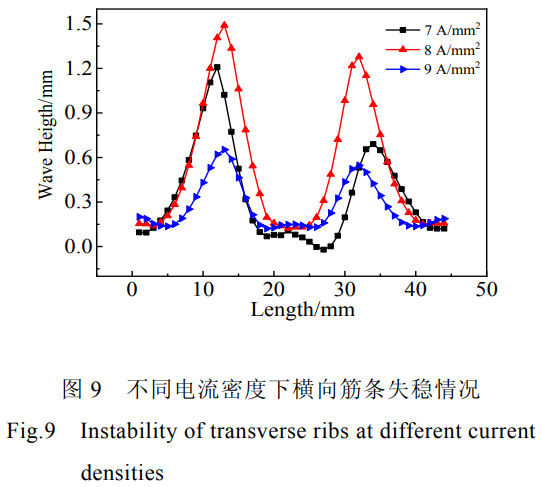
圖9所示電流密度7、8、9A/mm2下壁板橫向筋條沿x方向失穩(wěn)距離的整體情況。電流密度7、8、9A/mm2時(shí)橫向筋條最大失穩(wěn)距離分別為1.07、1.37、0.65mm。隨著電流密度增加,壁板筋條沿x方向失穩(wěn)距離先出現(xiàn)增大趨勢(shì)。壁板上筋條溫度升高,筋條處應(yīng)變較大,容易失穩(wěn)屈曲。隨著電流的進(jìn)一步加大,壁板筋條失穩(wěn)距離反而減小。溫度上升,壓彎所需的載荷減小,壁板筋條上的應(yīng)力減小,導(dǎo)致應(yīng)變相應(yīng)減小,失穩(wěn)屈曲程度減小。
2.4壁板壓彎半徑對(duì)失穩(wěn)屈曲的影響
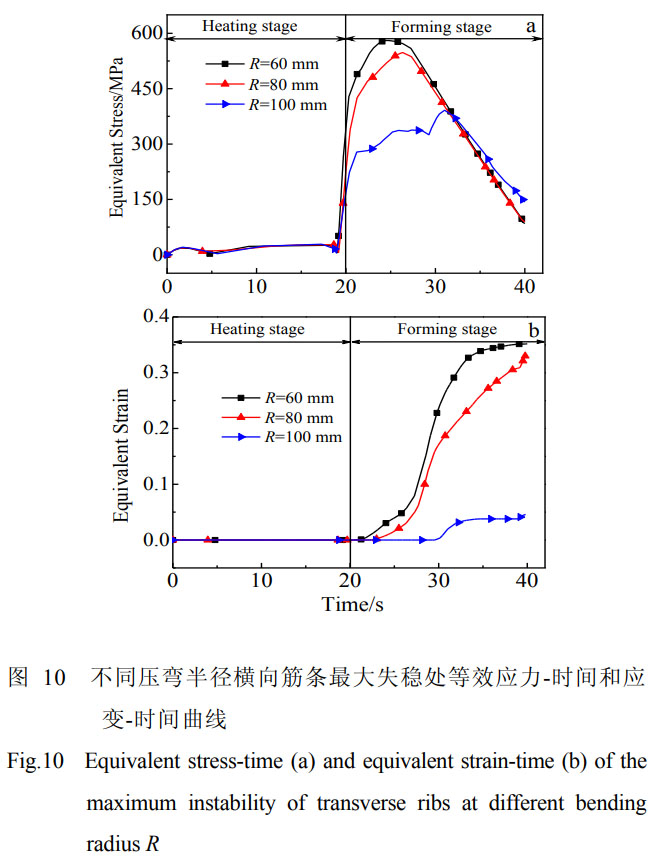
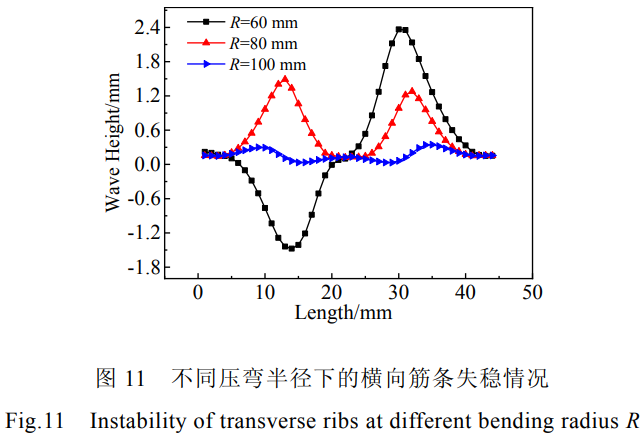
圖10所示為不同壓彎半徑下橫向筋條失穩(wěn)處等效應(yīng)力、等效應(yīng)變隨時(shí)間的變化曲線。由圖10a可知壓彎半徑增加時(shí),筋條應(yīng)力也越來(lái)越小,筋條的受力情況得到相應(yīng)的改善,筋條失穩(wěn)程度減小。圖10b為不同壓彎半徑下的筋條失穩(wěn)處等效應(yīng)變隨時(shí)間關(guān)系,壓彎半徑為60、80、100mm時(shí)筋條失穩(wěn)處的最終等效應(yīng)變分別為0.36、0.32、0.05,壓彎半徑增加,筋條的變形量隨之減小。由圖11不同壓彎半徑下的橫向筋條失穩(wěn)情況可知,整體壁板壓彎時(shí),隨著壓彎半徑的減小即變形量的增大,筋條失穩(wěn)越來(lái)越嚴(yán)重,橫向筋條失穩(wěn)程度越來(lái)越大,這與筋條失穩(wěn)處的等效應(yīng)變結(jié)果相吻合。壓彎半徑越小,橫向筋條失穩(wěn)屈曲程度越嚴(yán)重,筋條失穩(wěn)形成的半波的幅值越大。
2.5筋條寬高比對(duì)壁板失穩(wěn)屈曲的影響
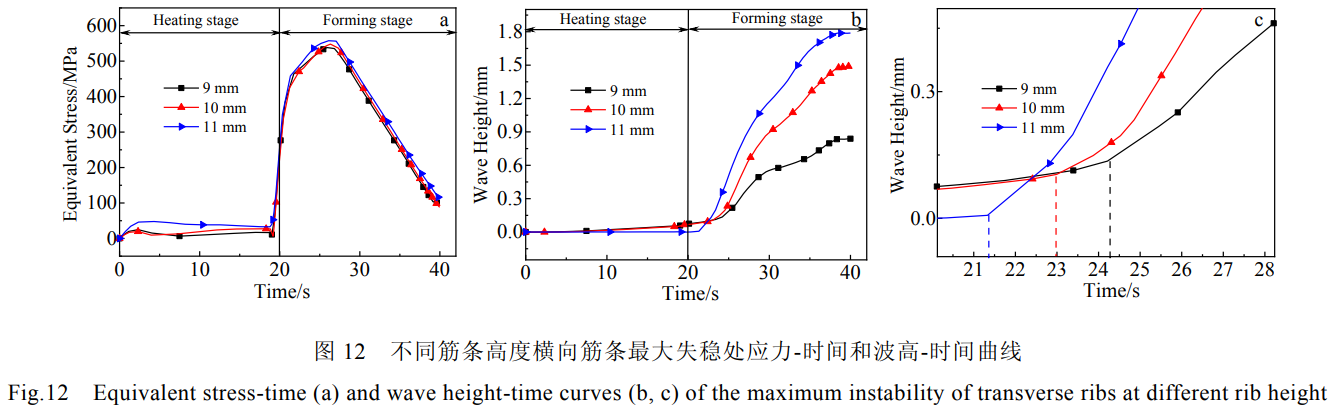
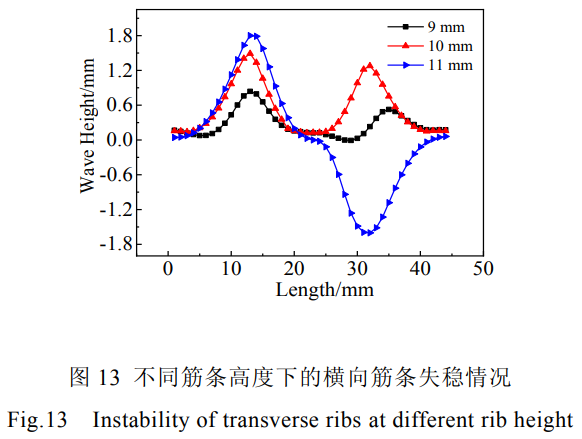
圖12所示為不同筋條高度橫向筋條最大失穩(wěn)處等效應(yīng)力、波高-時(shí)間曲線。由圖12a等效應(yīng)力-時(shí)間關(guān)系可知,筋條高度對(duì)橫向筋條最大失穩(wěn)處應(yīng)力無(wú)明顯影響。圖12b所示筋條寬高比對(duì)失穩(wěn)時(shí)刻的影響,圖12c為12b的局部放大圖,由圖可以看出,筋條高度為9~11mm時(shí)橫向筋條開(kāi)始發(fā)生失穩(wěn)的時(shí)間分別為24.21、23、21.33s,筋條高度越高,壁板開(kāi)始的失穩(wěn)的時(shí)間也越早。這表明筋條高度越高筋條失穩(wěn)時(shí)所需的臨界載荷越小,發(fā)生失穩(wěn)的時(shí)間越短,整體壁板筋條的穩(wěn)定性較差。圖13為不同筋條寬高比下的橫向筋條失穩(wěn)情況。由圖可知,在整體壁板筋條厚度不變,隨著筋條高度的增加,筋條失穩(wěn)屈曲程度越來(lái)越大。
2.6腹板厚度對(duì)筋條失穩(wěn)屈曲的影響
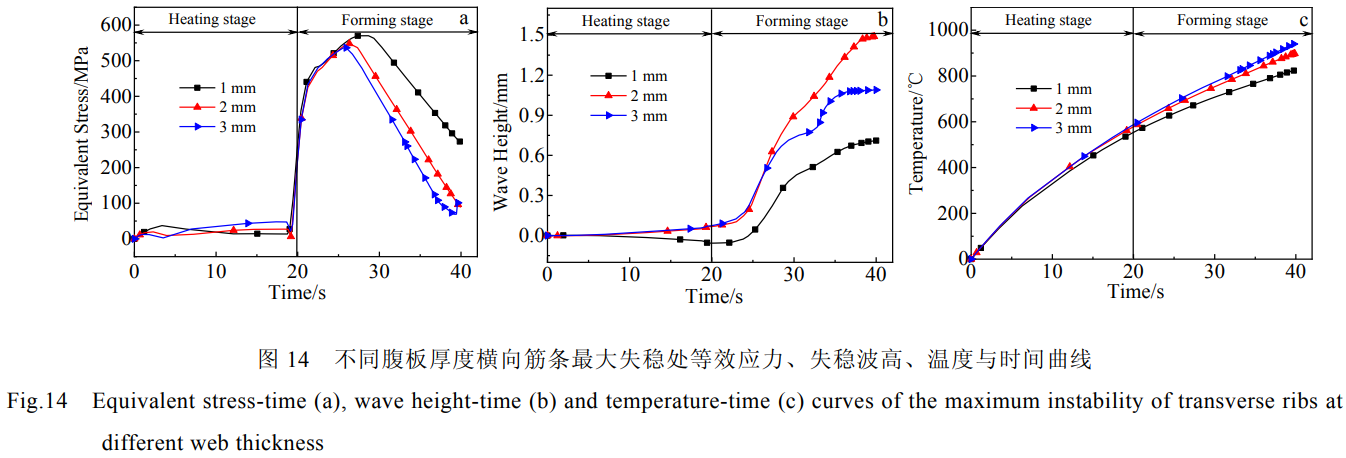
圖14所示為不同腹板厚度下橫向筋條最大失穩(wěn)處等效應(yīng)力、失穩(wěn)波高和溫度隨時(shí)間變化的曲線。由圖14a可知,不同腹板厚度的壁板在發(fā)生失穩(wěn)時(shí)的筋條處的應(yīng)力相同。由圖14b可以看出,腹板厚度不同,筋條失穩(wěn)時(shí)刻均發(fā)生在24s左右,無(wú)顯著差異,所以腹板厚度不會(huì)對(duì)筋條的失穩(wěn)時(shí)刻產(chǎn)生影響。由圖14c可知隨著腹板厚度的增加,壁板散熱減少,筋條溫度上升。
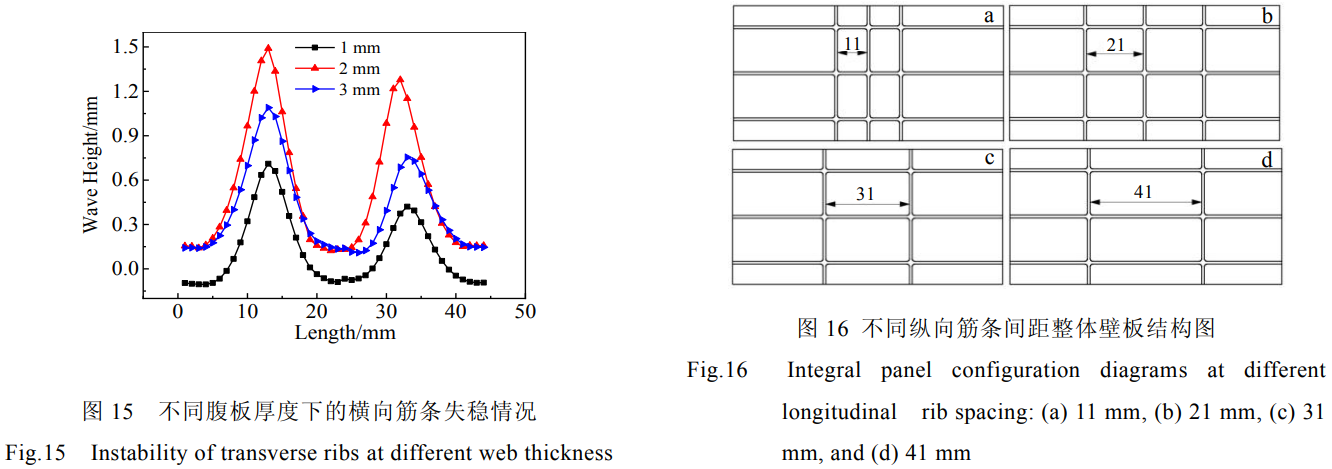
圖15為不同腹板厚度下的橫向筋條失穩(wěn)情況。腹板厚度增加,筋條失穩(wěn)屈曲程度加大,腹板厚度進(jìn)一步增加,壁板散熱減少,導(dǎo)致溫度上升,成形壁板所需載荷減小,壁板筋條上應(yīng)力減小,失穩(wěn)屈曲程度反而有所減小。腹板厚度其實(shí)影響筋條的溫度從而影響筋條失穩(wěn)的變化。
2.7縱向筋條間距對(duì)壁板失穩(wěn)屈曲的影響
圖16為不同縱向筋條間距整體壁板結(jié)構(gòu)圖。圖17所示為不同縱向筋條間距下橫向筋條最大失穩(wěn)處等效應(yīng)力、失穩(wěn)波高和溫度隨時(shí)間變化的曲線。由圖17可知縱向筋條間距為41mm時(shí)壁板筋條發(fā)生的失穩(wěn)時(shí)刻要比31mm早很多,從應(yīng)力-時(shí)間關(guān)系圖可以看出,縱向筋條間距為41mm時(shí)壁板筋條發(fā)生的失穩(wěn)時(shí)刻應(yīng)力也小很多,縱向筋條間距越大,橫向筋條穩(wěn)定性越差。縱向筋條的數(shù)量越少,電流向縱向筋條分流減小,橫向筋條溫度越高。筋條間距由31mm增至41mm而縱向筋條數(shù)量沒(méi)有變化時(shí),橫向筋條處溫度無(wú)明顯差別。
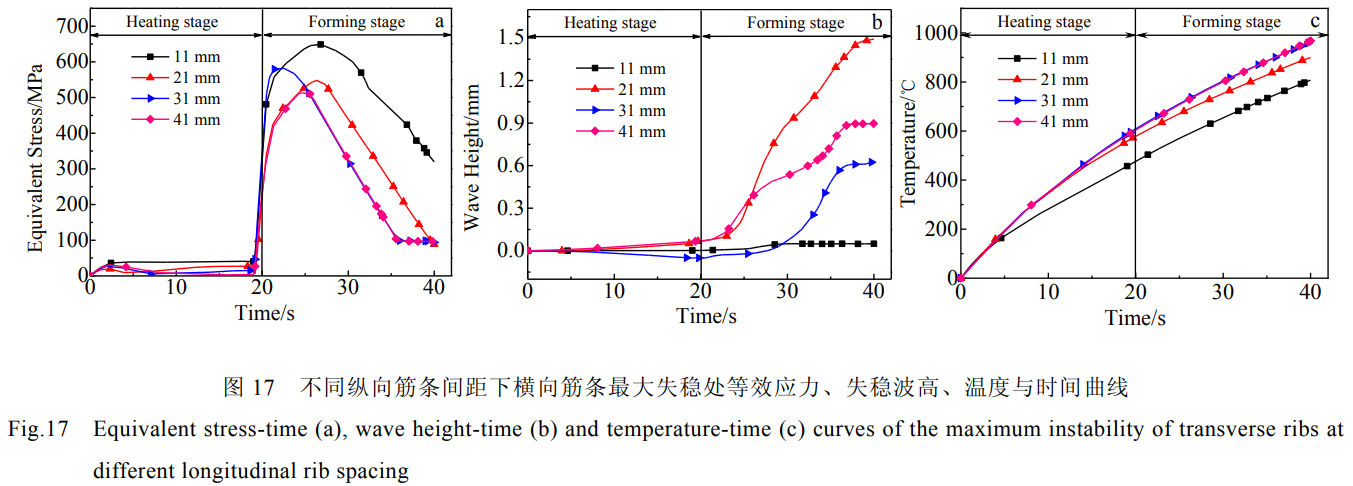
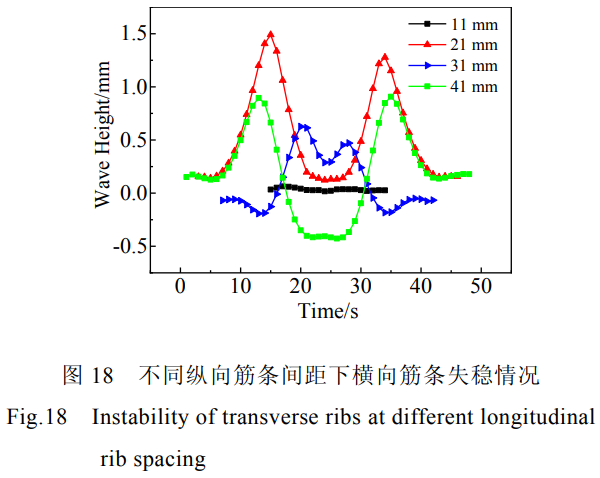
圖18所示為不同縱向筋條間距下的橫向筋條失穩(wěn)情況。由圖18可知,當(dāng)縱向筋條間距為11mm時(shí),整體壁板沒(méi)有產(chǎn)生失穩(wěn)彎曲,縱向筋條的存在阻礙了橫向筋條的變形,使整體壁板變形更均勻。筋條間距由21mm增至31mm時(shí),筋條溫度過(guò)高時(shí),且壓彎中心線處無(wú)縱向筋條,整體壁板中心處受力情況得到改善,失穩(wěn)程度反而減小。壓彎中心線處無(wú)縱向筋條時(shí),縱向筋條間距越大,橫向筋條越容易失穩(wěn),成形最終失穩(wěn)程度越大。
3、結(jié)論
建立了Ti55合金通電壓彎的電-熱-結(jié)構(gòu)多場(chǎng)耦合模擬模型并進(jìn)行模擬,對(duì)施加不同電流密度的整體壁板溫度場(chǎng)進(jìn)行分析,為獲得Ti55合金合適的成形溫度和避免溫度過(guò)高壁板氧化嚴(yán)重,在壁板端施加8A/mm2電流密度能獲得合適的壓彎溫度區(qū)間。
整體壁板隨著筋條高度的增加,筋條失穩(wěn)屈曲程度越來(lái)越大。筋條高度越高,筋條開(kāi)始的失穩(wěn)的時(shí)間也越早,筋條失穩(wěn)時(shí)所需的臨界載荷越小,發(fā)生失穩(wěn)的時(shí)間越短,筋條的穩(wěn)定性越差。
腹板厚度主要是影響筋條的溫度從而影響壁板壓彎過(guò)程中筋條的失穩(wěn),這與電流密度對(duì)筋條失穩(wěn)的影響相類似。
整體壁板縱向筋條間距增大,筋條穩(wěn)定性越差,筋條失穩(wěn)屈曲也越嚴(yán)重。
參考文獻(xiàn) References
[1] Zhao Anan (趙安安), Zhang Xianjie (張賢杰), Gao Guoqiang (高國(guó)強(qiáng)) et al. Acta Aeronautica et Astronautica Sinica (航空學(xué)報(bào))[J], 2019, 40 (2): 197
[2] Xu Aijun (許愛(ài)軍), Jia Yuerong (賈悅榮), Zhang Changxi (趙長(zhǎng)喜). Manned Spaceflight (載人航天)[J], 2017, 23 (5): 619
[3] Lang Lihui (郎利輝), Xu Aijun (許愛(ài)軍). Aviation Precision Manufacturing Technology (航空精密制造技術(shù))[J], 2011, 47 (2): 30
[4] Liu Zhangguang, Li Peijie, Xiong Liangtong et al. Materials Science & Engineering A [J], 2017, 680: 259
[5] Grimm Tyler J, Ragai Ihab. Procedia Manufacturing [J], 2019, 34: 118
[6] Liu Kai, Dong Xianghuai, Shi Wen et al. Journal of Shanghai Jiaotong University, Science [J], 2019, 24 (4): 409
[7] Yan Yu, Wang Haibo, Wan Min. Transactions of Nonferrous Metals Society of China [J], 2011, 21 (11): 2459
[8] Yan Yu, Wang Haibo, Wan Min. Computational Materials Science [J], 2011, 50 (7): 2232
[9] Mallela Upendra K, Upadhyay Akhil. Thin-Walled Structures [J], 2016, 102: 158
[10] Li Shen, Hu Zhiqiang, Benson Simon. Engineering Structures [J], 2019, 199: 109627
[11] Su Yuru, Guan Zhidong, Wang Xin et al. Chinese Journal of Aeronautics [J], 2019, 32 (3): 619
[12] Zhou Wenbin, Li Yong, Shi Zhusheng et al. International Journal of Mechanical Sciences [J], 2019, 161-162: 105024
[13] Liu Jinsong (劉勁松). Thesis for Doctorate (博士論文)[D]. Shenyang: Institute of Metal, Chinese Academy of Science, 2004: 27
[14] Ren Limei (任麗梅), Wang Zhongtang (王忠堂), Liu Jinsong (劉勁松) et al. Journal of Plasticity Engineering (塑性工程學(xué)報(bào))[J], 2003, 10 (5): 39
(原文標(biāo)題:Ti55鈦合金整體壁板電脈沖輔助壓彎成形失穩(wěn)研究)
無(wú)相關(guān)信息
